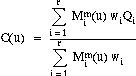Splines
A spline is a smoothed curve defined by input points and possibly by
additional vector constraints. The spline curve and its derivatives are
defined in the following illustration for a cubic spline segment.
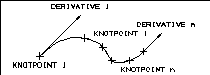
Figure Spline
There are many different types of spline curves. The ones used in
NX are Non-Uniform Rational B-spline curves, sometimes
referred to as "NURB" curves.
A Bezier curve is a B-spline curve that consists of only a single
segment. A B-Spline curve is a multi-segment curve represented by
a list of points called poles.
You can consider a spline curve as a list of Bezier curves, and a Bezier
curve as a special type of B-spline curve.
See the functions in the uf_modl.h chapter.
Degree of a Spline
A Spline has a degree. Degree is a mathematical concept; it actually
refers to the degree of the polynomial or rational functions used to
describe the curve.
A higher degree curve is stiffer in the sense that you have to move its
poles a long way to produce any appreciable change in the shape of
the curve. Lower degree curves are more pliable, and tend to follow
their poles much more closely.
In NX, the degree of a Spline must be between 1 and 24.
However, we recommend the use of cubics (a degree of 3) when
creating Splines. Creating lower degree curves results in faster
performance during subsequent operations such as machining,
display, etc. Using higher degree curves reduces the chance of
transferring data to other systems which may not support them. Also,
the creation of a high degree curve through many points may lead to
unpredictable results.
Degree of a Spline
To create a Bezier, single segment curve, set the degree to one less
than the number of points input.
B-Spline Curve Degree
For a B-spline curve, the degree is independent of the number of
points. You select the desired degree knowing that the minimum
number of points is one more than that degree.
points on curve
poles
Minimum/Maximum Number of Points
For a Bezier curve, the minimum number of points is two (minimum
degree of 1) and the maximum number of points is 25 (maximum
degree of 24 + 1). For a B-spline curve at least degree + 1 points
must be specified.
Creation Options
The system interprets the specified points in one of two ways: as
points through which the curve must pass; or as points defining the
location of the poles.
Points on Curve
Allows you to define a list of points through which the curve will pass.
The curve interpolates each specified point, as shown on Figure below.
When you use this option, you have control over the curve in the
sense that it will always pass through the points that you specify.
However, take note that specifying a high degree curve using this
option may produce unpredictable results.
Poles
Allows the system to interpret the specified points as poles of a control
polygon. In general, these poles do not lie on the resulting curve, as
shown in Figure below . Using the Poles option gives you much better
control of the overall shape and character of the curve since the
resulting curve follows the shape of the control polygon. Using Poles
gives you a much better chance of avoiding unwanted undulations
(reversals of curvature) in the curve.
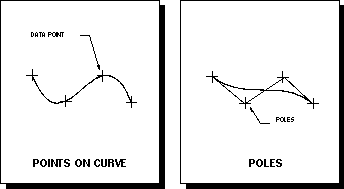
Figure Bezier: Points On Curve & Poles
Mathematical Composition of a Spline
A B-spline curve is a multi-segment polynomial curve represented
by an array of points (called poles), a sequence of parameter values
(called the Knot Sequence) and the degree of the curve.Let Pi (i = 1,
2,...,r) be the array of Poles defining the curve. Each Pole Pi is a
four-dimensional object, which is composed of a 3D point,
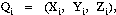
and a weight, wi,
where:
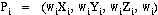
In the NX implementation, we require that the weights wi all
be strictly positive.
Now suppose that the curve has degree m. Then the knot sequence
will have r + m + 1 entries, which can be denoted by:
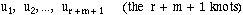
The knot sequence must be non-decreasing, i.e.
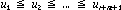
NX imposes restrictions on the knot sequence of a b-curve
to ensure the curve is smooth.
- The multiplicity of the end knots can be at most m+1.
- The multiplicity of the of each of the interior knots can be at
most m.
In other words, we require:
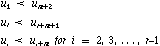
These restrictions guarantee that the curve is at least continuous in
position. Discontinuities in the first derivative are not handled reliably
by some NX applications. To minimize these types of
discontinuities, we recommend that all b-curve knot sequences
satisfy the stronger condition:
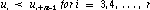
We also require a normalized knot sequence (scaled and shifted if
necessary), so that:
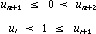
In most cases, it is advisable to make:
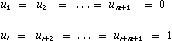
This will ensure that the curve starts at Q1 and ends at Qr , which
makes it easier for the user to edit. However, these conditions are
certainly not necessary.
Using the knots u1, u2,..., ur+m+1 we can construct r normalized
B-spline basis functions of degree m, which we denote by
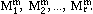
These basic functions are defined recursively, as
follows:
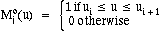
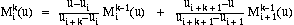
See References [1], [2] and [3] for further discussion of B-spline basis
functions.
Then the equation of the curve is:
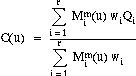
In fact, this curve is a non-uniform rational B-spline curve.
Several special cases are of interest:
- If the Wi are all equal to 1, then, since:
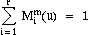
the equation of the curve reduces to:
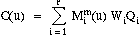
which is an ordinary (polynomial) B-spline curve.
- If, in addition, we have:
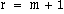
and if the knot sequence satisfy:
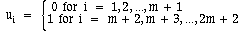
then the curve reduces to a single Bezier patch.

[1] Rogers and Adams
Mathematical Elements For Computer Graphics,
McGraw Hill, 1976
[2] Gerald Farin
Curves and Surfaces For Computer-Aided Geometric Design,
Academic Press, 1988
[3] de Boor
A Practical Guide To Splines
Springer-Verlag, 1978