Lets you create a Parabola.

Lets you create a Hyperbola.

The General Conic option lets you create conic sections by using either one of the various loft conic methods or the general conic equation. The resulting conic is either a circle, an ellipse, a parabola, or a hyperbola, depending on the mathematical results of the input data.

Conics are created mathematically by sectioning cones. The type of curve that results from the section depends on the angle at which the section passes through the cone (see the figure below). A conic curve is located with its center at the point you specify, in a plane parallel to the work plane (the XC-YC plane).

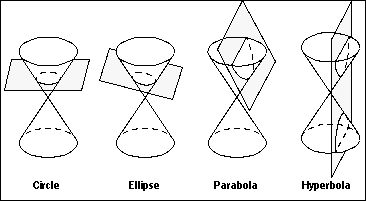
Specific types of conics are created when working with geometric constraints or certain types of applications. There are four types of conic curves you can create: arc/circle, ellipse, parabola and hyperbola. Each is a separate icon under curve creation. The General Conic option gives you another way to define ellipses, parabolas, and hyperbolas. An ellipse and a general conic are described using construction techniques (major and minor axes, end slopes, etc.). A parabola and hyperbola require more of a "textbook" definition (focal length; vertices; etc.).

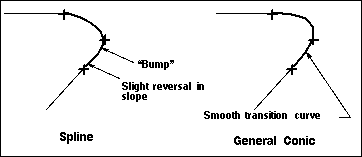
Conics curve in a single direction. In some instances they can be more useful than splines. One good use for conics is in blending transitions between two existing curves where reversals in slope (or bumps in the transition curve) are a problem (see the figure below).