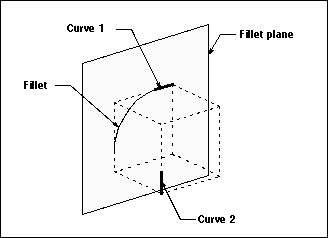
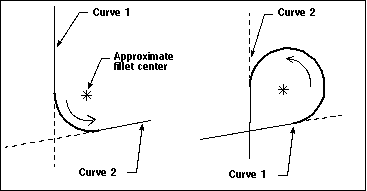
Constructs a fillet between two curves, including points, lines, circles, conics or splines. A two curve fillet is an arc generated in the counterclockwise direction from the first curve to the second. The fillet created by this method is tangent to both curves.

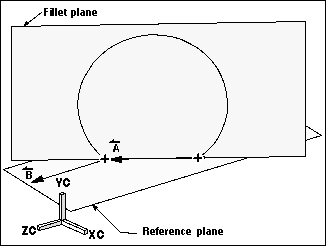
If a fillet is created between two points, it is created in a plane based on the location of the points. In the figure below, the reference plane is defined by a vector between each point (A) and the vector parallel with the ZC axis (B). The fillet is created in the plane containing each point and normal to the reference plane.

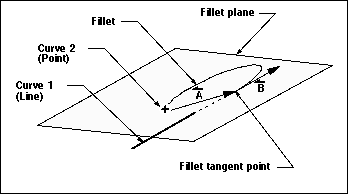
If only one curve is a point, the fillet plane is defined as the plane which contains the vector between the point and the fillet tangency point (A), and the tangent of the filleted object (B) (see the figure below). The fillet plane is totally independent of the WCS.

If neither curve is a point, the fillet plane is the plane that contains the tangent of the first curve. The plane is normal to the vector that is normal to both tangents. The two curves do not need to lie in the same plane and the fillet is completely independent of the WCS.